Your Damped natural frequency equation images are ready in this website. Damped natural frequency equation are a topic that is being searched for and liked by netizens today. You can Download the Damped natural frequency equation files here. Find and Download all free photos and vectors.
If you’re looking for damped natural frequency equation pictures information related to the damped natural frequency equation topic, you have pay a visit to the right blog. Our site always gives you hints for refferencing the maximum quality video and image content, please kindly search and locate more enlightening video articles and graphics that match your interests.
Damped Natural Frequency Equation. α R 2 L. From the graph T d is found to be 13 ms. 18 rows For damped forced vibrations three different frequencies have to be distinguished. This frequency can be calculated simply by the following relationship.
Calculating The Damping Ratio Zeta And The Undamped Natural Frequency Omega 0 Electrical Engineering Stack Exchange From electronics.stackexchange.com
Compare to the natural frequency and natural period of an undamped system. The larger the damping constant γ the smaller quasi-frequency and the longer the quasi-period become. From the graph T d is found to be 13 ms. Solution to the forced Damped Oscillator Equation. Recall that the angular frequency of a mass undergoing SHM is equal to the square root of the force constant divided by the mass. Is called the damping coefficient and.
UABtect2m Critically Damped System Over-damped System Underdamped System cc cr 2km2mω n cc cr General solution.
However response u to input F 0 cosωt may be large if damping is small and ω 0 - ω 0 in which case we have resonance. However response u to input F 0 cosωt may be large if damping is small and ω 0 - ω 0 in which case we have resonance. Therefore f d 113 ms d2π. Wnsqrtkm where k is the stiffness and m is the mass of the system. Show that a possible solution for the particle trajectory is rt Ac cos wit 1 where wi Vw - 72 with wo km as the natural frequency of the spring. If forcing frequency equals natural frequency of system ie ω ω 0 then our solution is.
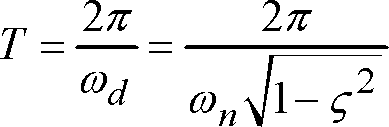Source: brown.edu
Eventually at the critical damping threshold when γ 4mk the quasi-frequency vanishes and the displacement becomes aperiodic becoming instead a critically damped. Damped natural frequency Formula Database Formula Sheet. However response u to input F 0 cosωt may be large if damping is small and ω 0 - ω 0 in which case we have resonance. 0 1 2 3 4 5 00 02 04 06 08. Y k 1 e ζ ω n t 1 ζ 2 P sin ω t Q cos ω t with ySS k ω ωn 1 ζ2 and as derived earlier in item 3 Q 1 ζ2.
Source: quora.com
Xt e2tc 1 c 2t. If forcing frequency equals natural frequency of system ie ω ω 0 then our solution is. Write x1 xt1 and x2 xt2. Damped natural frequency Formula Database Formula Sheet. Beginalignomega_d omega_n sqrt1 - zeta2 omega_n sqrtfrackm quad zeta fracc2 m.
Source: chegg.com
Where C and θare defined with reference to Eq29The damped natural frequency is related to the undamped natural frequency of Eq. Cosn t Xt e X tMd ζω ω ϕ 11c where 22 XM CC12and 2 1 tan C C ϕ Note that as t X. X1 ln x1 ln x2 ln. 0 1 2 3 4 5 00 02 04 06 08. ω t ϕ where the amplitude x 0 is a function of the driving angular frequency ω and is given by.
Source: itectec.com
Cosn t Xt e X tMd ζω ω ϕ 11c where 22 XM CC12and 2 1 tan C C ϕ Note that as t X. The solution to is given by the function. 2365 x t x 0 cos. Write x1 xt1 and x2 xt2. Because the roots are repeated the system is critically damped.
Source: electronics.stackexchange.com
The solution to is given by the function. ω t ϕ where the amplitude x 0 is a function of the driving angular frequency ω and is given by. The damped natural frequency or ringing frequency is found by determining the period of the oscillation T d and recalling the relation between period in seconds frequency in cycles per second and the conversion to circular frequency radianssecond. X1 ln x1 ln x2 ln. 32 the damping is characterized by the quantity γ having the dimension of frequency and the constant ω 0 represents the angular frequency of the system in the absence of damping and is called the natural frequency of the oscillator.
Source: chegg.com
Wnsqrtkm where k is the stiffness and m is the mass of the system. Eventually at the critical damping threshold when γ 4mk the quasi-frequency vanishes and the displacement becomes aperiodic becoming instead a critically damped. In general the solution is broken into two parts. This factors 2 2. UABtect2m Critically Damped System Over-damped System Underdamped System cc cr 2km2mω n cc cr General solution.
Source: quora.com
This frequency can be calculated simply by the following relationship. All are based on the observation that the left-hand side of this equation is a linearoperatoron q Lq. Displaystyleomegasqrt frac 1 L C-frac R 2 4 L 2 ω LC 1. The solution to is given by the function. Formulas for natural frequency Undamped natural frequency of system with stiffness K and mass M fn 1 2π K M Damped natural frequency fd n 1 ξ 2 This shows that the damped natural frequency of a structure with 5 damping will only be 01 lower than the undamped natural frequency.
Source: vortarus.com
ω t ϕ where the amplitude x 0 is a function of the driving angular frequency ω and is given by. 0 undamped natural frequency k m ω 13 damping constant 2 b m β 14 which is related to the fraction of critical damping ς by βως0. ωω ζdn is the system damped natural frequency. Beginalignomega_d omega_n sqrt1 - zeta2 omega_n sqrtfrackm quad zeta fracc2 m. ω 1 L C R 2 4 L 2.
Source: brown.edu
Motion u remains bounded if damping present. Xt e2tc 1 c 2t. Damped Harmonic Motion If the spring is subject to friction Newtons Equation becomes m da2 de -kx - 2mg d2 dl where is the coefficient of friction. Damped natural frequency Formula Database Formula Sheet. The homogeneous solution which solves the equation 2.
Source: brainkart.com
Compare to the natural frequency and natural period of an undamped system. The maximum values occur when ωt is some multiple of π and thus we have cos ωt 1 and sin ωt 0. 0 1 2 3 4 5 00 02 04 06 08. UABtect2m Critically Damped System Over-damped System Underdamped System cc cr 2km2mω n cc cr General solution. Displaystyleomega ω is given by.
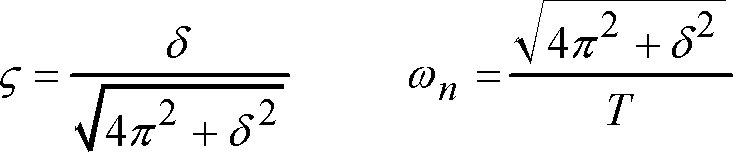Source: brown.edu
Is called the damping coefficient and. Cosn t Xt e X tMd ζω ω ϕ 11c where 22 XM CC12and 2 1 tan C C ϕ Note that as t X. The difference of their natural logarithms is the logarithmic decrement. Beginalignomega_d omega_n sqrt1 - zeta2 omega_n sqrtfrackm quad zeta fracc2 m. α R 2 L.
Source: study.com
T2 t1 We can also measure the ratio of the value of x at two successive maxima. ω 1 L C R 2 4 L 2. The solution to is given by the function. So x t e 2t 1 2t. Equation 32 is the differential equation of the damped oscillator.
Source: chegg.com
If the forcing frequency is close to the natural frequency of the system and the system. Cosn t Xt e X tMd ζω ω ϕ 11c where 22 XM CC12and 2 1 tan C C ϕ Note that as t X. Therefore f d 113 ms d2π. This is often referred to as the natural angular frequency which is represented as omega_0 sqrtfrackm ldotp label1525 The angular frequency for damped harmonic motion becomes. Wnsqrtkm where k is the stiffness and m is the mass of the system.
Source: chegg.com
T2 t1 We can also measure the ratio of the value of x at two successive maxima. From the graph T d is found to be 13 ms. It is easy to see that in Eq. At time t 0 the initial conditions are VV X X0 and 0 oo Then 00 10 2and n d VX CX C ζω ω 11b Equation 11 representing the system response can also be written as. If the forcing frequency is close to the natural frequency of the system and the system.
Source: chegg.com
We derive the solution to Equation 2364 in Appendix 23E. 32 the damping is characterized by the quantity γ having the dimension of frequency and the constant ω 0 represents the angular frequency of the system in the absence of damping and is called the natural frequency of the oscillator. ωω ζdn is the system damped natural frequency. The difference of their natural logarithms is the logarithmic decrement. 0 1 2 3 4 5 00 02 04 06 08.
Source: electronics.stackexchange.com
ω t ϕ where the amplitude x 0 is a function of the driving angular frequency ω and is given by. S2 4s 4 0. Where C and θare defined with reference to Eq29The damped natural frequency is related to the undamped natural frequency of Eq. 15 Equation 12 is a 2nd order linear differential equation and its solution is widely known. Recall that the angular frequency of a mass undergoing SHM is equal to the square root of the force constant divided by the mass.
Source: researchgate.net
In general the solution is broken into two parts. In all the preceding equations are. The intial conditions are satisfied when c 1 1 c 2 2. In general the solution is broken into two parts. 0 undamped natural frequency k m ω 13 damping constant 2 b m β 14 which is related to the fraction of critical damping ς by βως0.
Source: coursehero.com
T2 t1 We can also measure the ratio of the value of x at two successive maxima. Equation 32 is the differential equation of the damped oscillator. ω t ϕ where the amplitude x 0 is a function of the driving angular frequency ω and is given by. S2 4s 4 0. Wnsqrtkm where k is the stiffness and m is the mass of the system.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title damped natural frequency equation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
